힙이란 무엇일까?
- 최댓값 및 최솟값을 구하는 연산을 빠르게 수행하기 위해 고안된 완전 이진 트리를 기반으로 한 자료구조이다.
그렇다면 완전 이진 트리란 무엇일까?
- 우선 트리는 계층적 관계를 표현하는, 노드로 이루어진 비선형 자료구조이다.
이진 트리는 모든 노드의 자식 노드가 2개 이하인 트리 구조를 말한다.

위와 같은 이진 트리 구조에서 마지막 디그리를 제외하고 모든 노드가 채워져 있는 구조를 완전 이진 트리라고 한다.
위 트리 그래프도 완전 이진 트리 형태이다.
이제 다시 힙에 대해 알아보자.
힙에는 두 가지 종류가 있다.
부모 노드의 키 값이 자식노드의 키 값보다 항상 큰 힙을 최대 힙,

부모 노드의 키 값이 자식노드의 키 값보다 항상 작은 힙을 최소 힙이라고 부른다.

최대 힙과 최소 힙에서 대소의 관계는 부모 노드와 자식 노드 간에만 성립하며, 형제 사이에서는 성립하지 않는다.
힙 생성
힙 정렬을 하기 위해선 정렬햐고자 하는 배열을 힙으로 만들어야한다. 간단하게 아래 사진처럼 배열 순서에 따라 순차적으로 힙을 생성할 수 있다. 이진 트리의 부모 노드 A[k]가 A[2k]와 A[2k+1]을 자식 노드로 갖는 성질 때문이다.


힙 정렬
위 그림은 최소 힙의 조건을 만족하는 것을 확인할 수 있다. 해당 힙으로 힙 정렬을 실행해보겠다.

먼저 힙의 최솟값(3)과 맨 끝단의 마지막 노드(7)를 교환해준다.
최솟값(3)을 힙에서 제거한다.
최소 힙의 성질이 깨졌기 때문에 다시 최소 힙으로 만들어 주어야한다.
왼쪽 자식 노드와 오른쪽 자식 노드 중, 더 작은 자식 노드인 4를 7과 교환해준다.
다시 최소힙이 성립되었다.
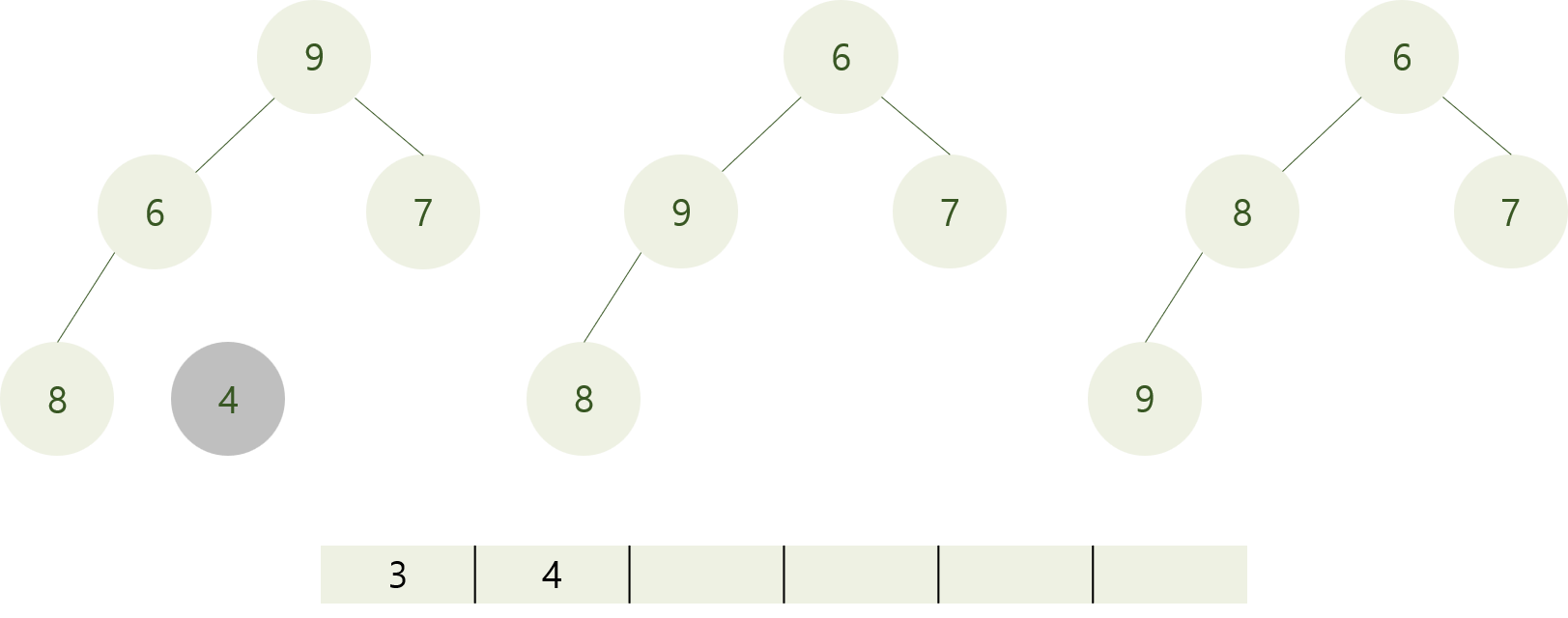
또 다시 가장 말단의 자식 노드(9)와 최솟값(4)을 교환해준다.
최솟값(4)를 힙에서 제거한다.
다시 힙을 최소 힙으로 만들어 준다.
좌,우 자식 노드 중 더 작은 값인 6을 9와 교환한다. 여전히 최소힙을 만족시키지 못한다.
한 번 더 자식 노드(8)와 9를 교환해준다. 이제 최소 힙이 성립되었다.
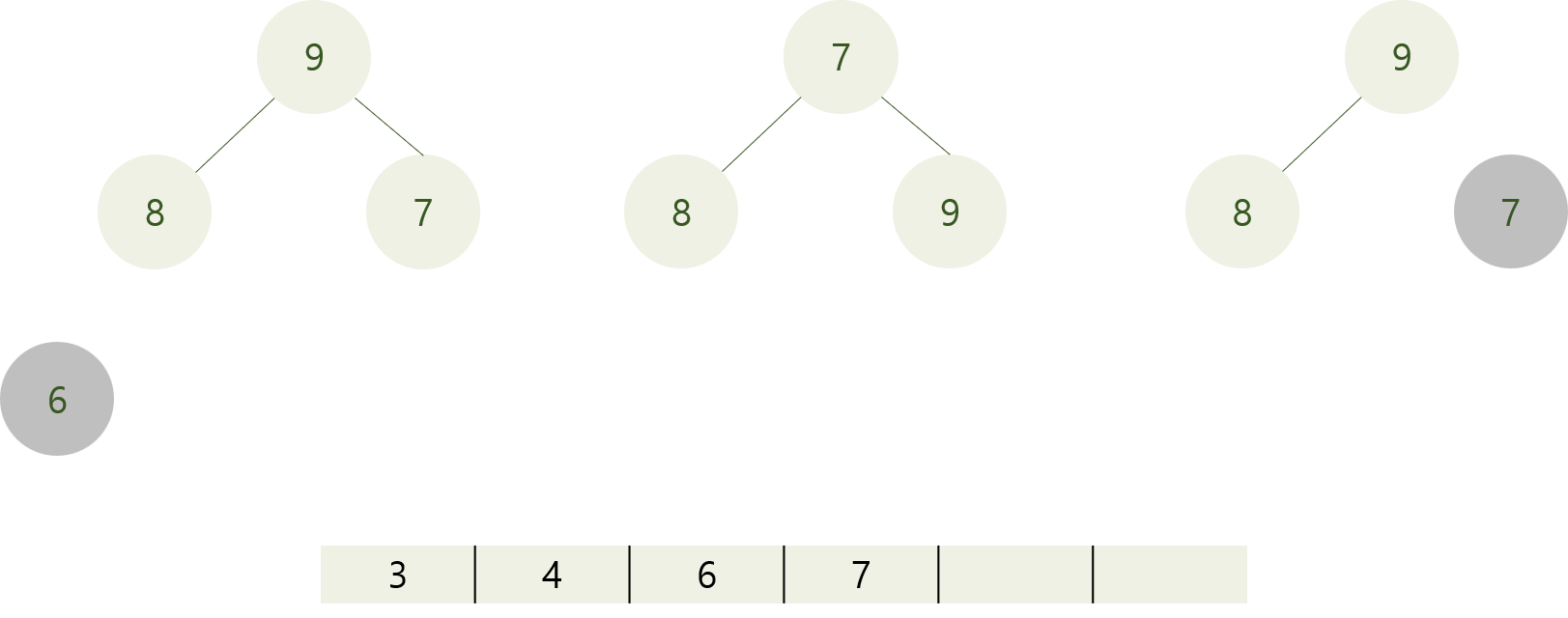
최솟값(6)과 말단 노드 값(9)을 교환해주고, 최솟값(6)을 제거한다.
7과 9를 교환해 최소 힙으로 만들어주고, 다시 최솟값과 말단 노드와 교환, 최솟값 제거.
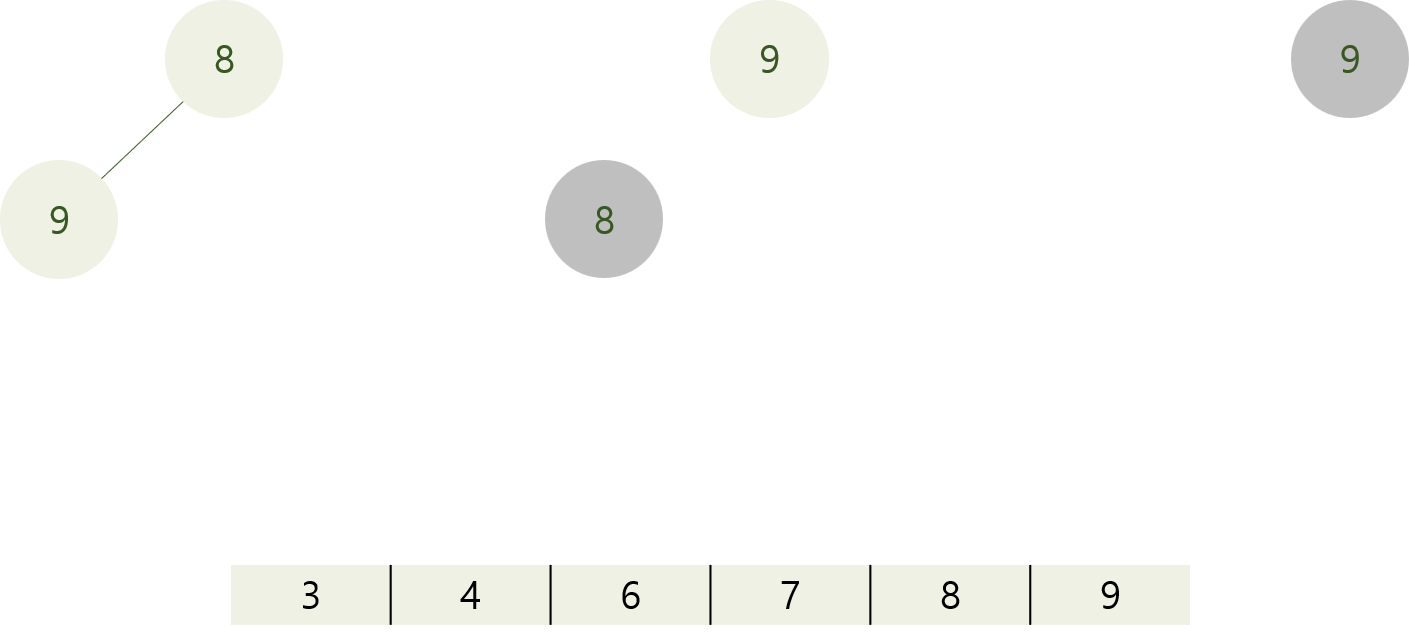
8과 9를 교환해 최소 힙으로 만들어주고, 최솟값(8)과 끝단 노드를 교환.
8을 제거.
하나 남은 9 제거.
이렇게 힙 정렬 과정이 끝이 났다.
'알고리즘' 카테고리의 다른 글
| [BOJ] 13565 침투 - python (0) | 2022.03.23 |
|---|---|
| [개념] BFS(Breadth-First Search) - python (1) | 2022.03.20 |
| [BOJ] 1946 신입 사원 - python (0) | 2022.03.16 |
| [BOJ] 2108 통계학 - python (0) | 2022.03.15 |
| [BOJ] 1302 베스트 셀러 - python (0) | 2022.03.04 |
